Mathematics & Beauty
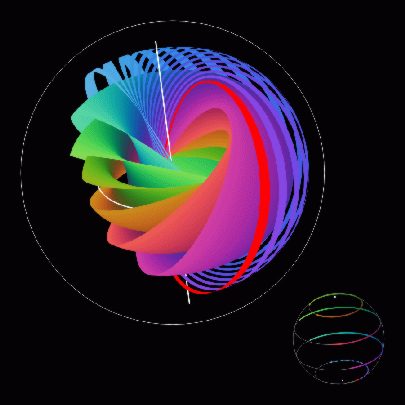
| The figure (created by Ken Shoemake) is a visualization of the Hopf fibration of the three sphere over the two sphere. It shows both S^3 and S^2, and visually connect fibers to base points. For each point on S^2 there is a unique RGB color by putting the sphere inside a color cube. Each fiber is colored uniformly with the color of the base point. To display S^3, the author punctured and flattened it to B^3 using a unit quaternions for the S^3 and took their logarithms (the inverse of the exponential map at 1+0i+0j+0k) for B^3. To show structure, a few arcs of lattitude as base points were chosen to give sliced tori for fibers. The coloring is continuous on S^2, so it is also continuous and delightful in the fibers. It shows nesting tori, linking fibers, base-fiber relations.A visualization of the fibering of RP3 by S1 over S2 is explored in detail in the article by Rick Kreminski in Mathematics in Education and Research , vol. 6, no. 1 and his wonderful graphic which was on the cover of the Notices of the AMS in May 1997 can be found at the web site: Hopf fibration video |

This Viking ship was created by Pontus Axelsson and Fredrik Sandberg (Using MATLAB) of Department of Numerical Analysis and Computing Science of the Royal Institute of Technology in Stockholm, Sweden. This boat started its life as a rowboat for a project in a numerical methods course, but it grew until it was a fully-rigged Viking ship. There is also a movie (98K, mpg) of the boat in motion!
More mathematical imaginary on the AMS Website ( www.ams.org/mathimagery), which mathematicians and artists create stunning works in all media and explore the visualization of mathematics.
video clips: Math is Beautiful
How to Turn a Sphere Inside Out: Part IPart II
