1) For a simple thermodynamic system show that:
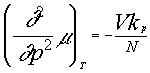
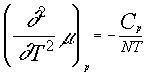
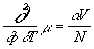
2) Compute the slope of the coexistence line dp/dT in Pa/K for water in the following cases: (a) boiling under atmospheric pressure: T = 100 C, latent heat l = 540cal/g, vgas = 1.6729 l/g, vliq = 1.044*10-3 l/g; (b) freezing under atmospheric pressure: T = 0 C, latent heat l = 80 cal/g, vice = 1.25 cm3/g, vliq = 1.0 cm3/g.
DUE:
HOMEWORK #2
1) Study the accuracy of the Stirling approximation by computing the fractional error:
e (N) = 1 – (NlnN – N)/ln(N!)
for N = 1, 2, …10. Sketch e (N).
2) (a) Consider four objects {a, b, c, d}. List all permutations of these 4 objects. How many permutations did you find?
(b) You have four identical (indistinguishable) marbles and three boxes. List all possible ways of distributing the 4 marbles in the 3 boxes. How many ways there are?
DUE:
HOMEWORK #3
CALLEN: CH.15, SECT.2, PR.2
For lead U � 3NkBT for temperatures above about 90K, while for diamond this holds for temperatures above about 2000K. By using the Einstein model estimate the angular frequency w , and the elastic constant k for Pb and C (diamond).
DUE:
HOMEWORK #4
For the two-state model graph: (a) the fundamental equation s(u); (b) T(u). Discuss the negative temperature phenomenon.
DUE:
HOMEWORK #5
CALLEN: CH.16, SECT.2, PR.6
Calculate the fractional energy fluctuation for the Einstein crystal and for an ideal gas. Hint: use Gibbs – Einstein formula.
DUE:
HOMEWORK #6
Calculate the partition function Z and the Helmholtz free energy F for the classical crystal by using the canonical ensemble. (b) Calculate the energy, the entropy and the heat capacity.
DUE:
Homework #7
(a) Prove the Wien displacement law: l m*T = 2.898*10-3 m*K, where l m is the wavelength for which the spectral energy density dU/dl is maximum.
(b) Compute l m at room temperature. Check it is in the infrared part of the spectrum.
(c) The maximum spectral energy density dU/dl in the sun�s spectrum occurs at a wavelength of 4700A. What is the surface temperature of the sun?
(d) Compute the heat capacity of radiation inside a container of volume 1liter at room temperature.
DUE:
HOMEWORK #8
For each statistical mechanics ensemble (microcanonical, canonical, grandcanonical) prove the following formula for the entropy:
S = -kB S Pj ln(Pj)
where Pj is the probability of microstate j.
2) The grand canonical potential W for an ideal gas is: W = -kBT*V*exp(m /kBT)*1/l T3
Show: (a) U = 3pV/2; (b) pV = NkBT. (c) Determine the fundamental equation: m = m (T,p).
DUE:
HOMEWORK #9
Consider the ideal Fermi gas. Prove the following formula for the entropy:
S = -kB S [nj ln(nj ) + (1 – nj )ln(1 – nj)]
where nj is the average number of fermions occupying quantum state #j.
By using the free-electron approximation for metals compute: the Fermi energy in eV, the Fermi temperature in K, the pressure in Pa, the bulk modulus in Pa, for gold. The number of free electrons per volume is N/V = 5.9*1028m-3.
DUE:
HOMEWORK #10
1. Consider the ideal Bose-Einstein gas. Prove the following formula for the entropy:
S = -kB S [nj ln(nj ) – (1 + nj )ln(1 + nj)]
where nj is the average number of bosons occupying quantum state #j.
2. Compute the Bose condensation temperature for He4 if N/(gV) = 2.2*1028m-3 and m = 6.65*10-27 Kg.
3. Consider the ideal Bose-Einstein gas of ultrarelativistic particles. The energy and momentum are related through the relativistic formula e = pc. (a) Determine the grand-canonical potential W , the energy U, and the number of bosons N as functions of T, V, and m . (b) Determine the condensation temperature TC as a function of N/V.
DUE:
