Research – Ryan, Shawn D.

External Funding

2023-2026 USDA-NIFA (PI D. Munther, Co-PI S. D. Ryan, Co-PI C. Kothapalli) $498,177.60

2023-2027 NSF REU Grant (PI J. Bickel, K. Streletzky, S. D. Ryan Senior Personnel) $365,000

2017-Present Ohio SuperComputing Center Grant PFS0230-1 (PI S. D. Ryan) $1000 annually

2017 Public Health Agency of Canada Grant #582090 (PI D. Munther, Co-PI S. D. Ryan)

Awards

2023-2024 CSU Distinguished Faculty Award for Teaching

2023-2024 Jearl D. Walker Outstanding Teaching Award

2018,2020,2023 CSU Provost Faculty Merit Award for Teaching and Research

2018, 2020, 2022 CSU Alumni Assoc. Golden Apple Award

2021-2022 Faculty Champion Award from CSU Center for Faculty Excellence

2021 CSU OER Faculty Letter of Recognition

2015 Kent St Certificate for Dedicated Service and Outstanding Contribution to Student Success

2014 Penn State Pritchard Dissertation Award (Outstanding Math Dissertation at PSU)

2012 Penn State Department of Mathematics Teaching Award

2009-2014 Penn State University Graduate Research Fellowship

2009 Penn State August and Ruth Homeyer Graduate Fellowship

2008 Barry M. Goldwater Scholar

2007 Alberta M. and William C. King Outstanding Math Jr/Sr at U. Akron

2006 Dr. Mary E. Maxwell Outstanding Freshman in Mathematics at U. Akron

2005 Univeristy of Akron Honors Scholarship of Excellence Award

Research Group

Research Group

CSU Center for Applied Data Analysis and Modeling (ADAM)

Press

Research Topics

I am an applied mathematician who specializes in solving problems originating at the interface of mathematics, physics and biology taking advantage of the tools and data present in each field to build better models. The unifying theme among all my research topics is interactions (interparticle, molecular, fluid-mediated, …) leading to the emergence of natural phenomena. My work consists of developing differential equations based models for biosystems and materials that predict the emergence of collective behavior and result in dramatic changes in the system’s effective properties. Mathematical analysis and simulations are used to uncover deeper understanding of the systems under consideration.

Collective Motion in Active Biosystems

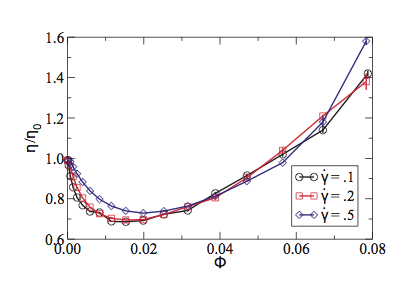
Effective Viscosity: The viscosity of a suspension of swimming bacteria can be investigated analytically and numerically. In recent work (PRE 2011), a simple model that allows for efficient computation for a large number of bacteria is proposed. The calculations show that long-range hydrodynamic interactions, intrinsic to self-locomoting objects in a viscous fluid, result in a dramatic reduction of the effective viscosity. In agreement with experiments on suspensions of Bacillus subtilis, one can show that the viscosity reduction is related to the onset of large-scale collective motion due to interactions between the swimmers. Numerical simulations reveal that the viscosity reduction occurs only for relatively low concentrations of swimmers: Further increases of the concentration yield an increase of the viscosity. An explicit asymptotic formula for the effective viscosity in terms of known physical parameters can then be derived and this formula shows that hydrodynamic interactions are manifested as self-induced noise in the absence of any explicit stochasticity in the system.

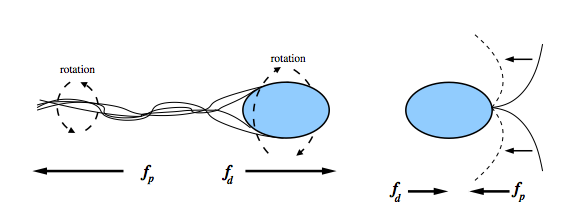
Global Solvability Suspensions of self-propelled microscopic particles, such as swimming bacteria, exhibit collective motion leading to remarkable experimentally observable macroscopic properties. Rigorous mathematical analysis of this emergent behavior can provide significant insight into the mechanisms behind these experimental observations; however, there are many theoretical questions remaining unanswered. In recent work (SIAM MMS 2013), a coupled PDE/ODE system first introduced in the physics literature and used to investigate numerically the effective viscosity of a bacterial suspension is studied. Then the kinetic theory associated with the coupled system, which is designed to capture the long-time behavior of a Stokesian suspension of point force dipoles (infinitesimal spheroids representing self-propelled particles) with Lennard-Jones–type repulsion is analyzed. A planar shear background flow is imposed on the suspension through the novel use of Lees–Edwards quasi-periodic boundary conditions (see below) applied to a representative volume. One can then show the existence and uniqueness of solutions for all time to the equations of motion for particle configurations—dipole orientations and relative positions. This result follows from first establishing the regularity of the solution to the fluid equations. The existence and uniqueness result allows one to define the Liouville equation for the probability density of configurations. Then this probability density is shown to define the average bulk stress in the suspension underlying the definition of many macroscopic quantities of interest, in particular the effective viscosity. These effective properties are determined by microscopic interactions highlighting the multiscale nature of this work.

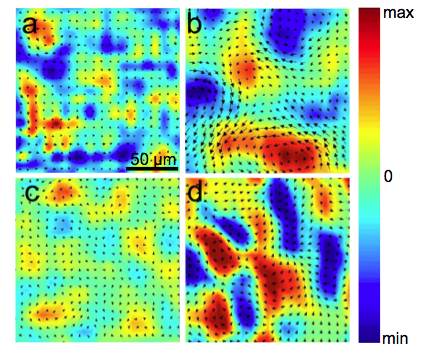
Collective Motion The study of collective motion in bacterial suspensions has been of significant recent interest. To better understand the non-trivial spatio-temporal correlations emerging in the course of collective swimming in suspensions of motile bacteria, a simple model is employed: a bacterium is represented as a force dipole with size, through the use of a short-range repelling potential, and shape. The model emphasizes two fundamental mechanisms: dipolar hydrodynamic interactions and short-range bacterial collisions. Using direct particle simulations validated by a dedicated experiment, one can show that changing the swimming speed or concentration alters the time scale of sustained collective motion, consistent with experiment. Also, the correlation length in the collective state is almost constant as concentration and swimming speed change even though increasing each greatly increases the input of energy to the system. It is demonstrated that the particle shape is critical for the onset of collective effects. In addition, new experimental results are presented illustrating the onset of collective motion with an ultrasound technique.

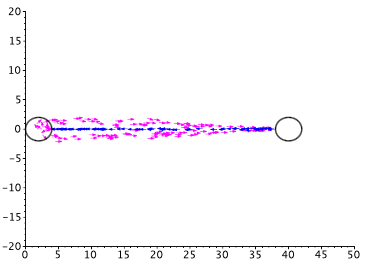
Social Insect Behavior This area focuses on the investigation of collective dynamics observed during ant foraging and raiding. The basic idea is to start with an individual based ODE model derived from first principles (balance of forces). In nature ants perform a random walk in search of food. Once food is found ants returning to the nest with food begin to lay a trail consisting of a chemical gradient to direct other ants toward the food. Upon returning to the nest they become foragers once again, but now follow the chemical trail to efficiently recover the needed resources. This entire cycle of foraging an returning is referred to as a raid. The model I recently developed has shown striking collective features similar to what has been observed in recent experiment. Namely, self-organization of the ants into a collective state exhibiting local traffic flow. In particular, the formation of three lanes: two outside lanes for foragers and one central lane for ants returning with food (right). The two main features are the different equations of motion for foraging ants and returning ants (due to different social and environmental cues) and the coupling of the equations of motion with a reaction-diffusion PDE for pheromone deposition. One can also derive a continuum PDE model for the ant density (In progress).

Materials Science, Liquid Crystals

Foam Coarsening This work, done in collaboration with KSU postdoc mentors Xiaoyu Zheng (Math) and Peter-Palffy Muhoray (LCI), concerned with developing a kinematic model for the evolution of a foam on the sphere (left). The main result is to develop an effective von Neumann relation on the sphere

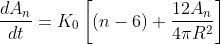
where A_n is the area of an $n$-sided cell/bubble, K₀ is a physical constant proportional to surface tension, R is the radius of the sphere, and the final term is the correction added to account for moving from 2D to 3D.

The remarkable property of the von Neumann law in 2D is that the change in area of a cell only depends on the number of sides (right), not on a cell’s size, but this property is lost in 3D. In the 2D case the 6-sided cells remain stationary while cells with less than six sides shrink to zero and cells with more than six sides grow quickly. The key question in moving to the sphere is that there are no longer any stationary states, so what will happen in the longtime? Also, one must accurately account for topological events such as the disappearance of cells and the exchange of boundaries between neighboring cells. The von Neumann law was recently cited by Richard James as a “historical touchstone” of material science and we hope to derive further results through numerical simulations on the sphere. This requires a deep understanding of both physics and mathematics.

Ginzburg-Landau Superconductivity

This work quantifies the effect of randomness in columnar defect locations (pinning sites) on the distribution of vortices. We develop an analytical method, based on the method of functional equations, for finding the vortex distribution given arbitrary defect locations. The random setting is studied by implementing a numerical algorithm of random walks for increased randomness starting from a periodic lattice of defects. Through simulations we identify three fundamental differences; namely, as randomness increases the interface becomes more fractal, the subdomains containing vor- tices move closer to the sample boundary, and the critical magnetic field for the onset of hole vortices decreases. These results fundamentally change how the traditional magnetic field–temperature phase diagram is viewed in the presence of columnar defects. This work highlights the delicate balance be- tween vortex-vortex, vortex-defect, and confinement within a finite system in determining the effective vortex distribution.

Graphene Sheet Deformation

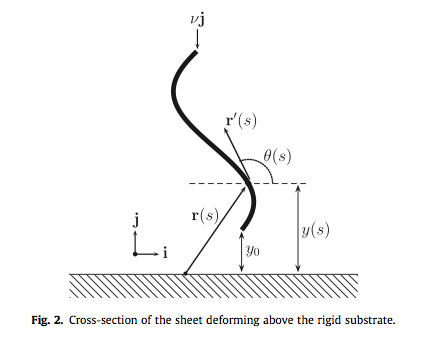
The work on graphene sheet deformation was done in collaboration with Assoc. Professors D. Golovaty and J. P. Wilber. This work focuses on analyzing a coupled ODE model for an interacting graphene sheet suspended above a rigid graphene substrate. Graphene has received recent popularity given the Nobel prize win in 2010 by Andre Geim and Konstantin Novoselov for extracting the single layer thick carbon sheet. This work resulted in my Masters thesis and two publications. In these works we study a variation on the classical problem of the buckling of an elastica modeling a nanoscale sheet that interacts with a rigid substrate by intermolecular van der Waals forces. This study is motivated by similar bending problems in nanomechanics. One can formulate a buckling problem in which the sheet is perpendicular to the substrate and a load is applied to the edge of the sheet further from the substrate. After identifying a trivial branch of sheet configurations, we combined numerical and asymptotic analysis to determine the stability and bifurcations of solutions along this branch.

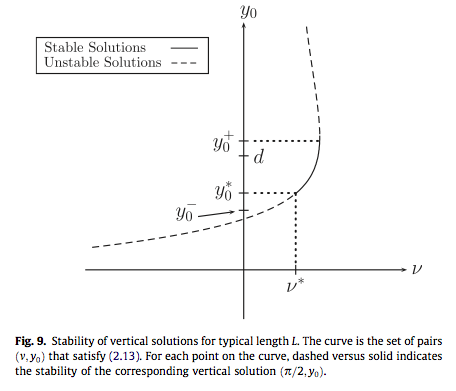
The boundary-layer problem that arises if the length of the sheet is large compared to the characteristic length over which the van der Waals interaction is significant is studied. This approach reveals that for large length sheets the pulling and pushing bifurcations arise by different mechanisms. The pulling bifurcations arise in the inner problem if the applied load is leading order. These bifurcations are novel and are tied to the van der Waals interaction between the sheet and the substrate. The countable number of pushing bifurcations arise in the outer problem if the applied load is of order epsilon^2 where epsilon is a small perturbation of the configuration, in which case this is a version of the classical Euler buckling problem.